Probeer jij wel eens een stelling vanuit het standpunt van een ander te bekijken? Vandaag gaan we een wiskundig ding beschrijven dat net zo’n grote uitdaging kan zijn voor de beginnende natuurkundige: de tensor. Tensoren spelen een erg belangrijke rol in allerlei takken van de natuurkunde. In deze post leg ik je uit wat een tensor intuïtief voorstelt, kijken we naar de wat meer wiskundige definitie van een tensor, en bespreken we toepassingen.

Intuïtie
Allereerst: wat stelt een tensor intuïtief voor? Wel, toevallig heb ik een tensor in huis. Of beter gezegd: een analogie voor een tensor, namelijk een cilinder. Die zie je in de afbeelding hierboven. In de linker afbeelding lijkt de cilinder een cirkel. Maar als ik vervolgens om de cilinder draai, dan lijkt het opeens een rechthoek te worden. En ik kan natuurlijk ook nog andere invalshoeken bekijken waarin de vorm van de cilinder lijkt te veranderen. LIJKT, want de vorm van de cilinder maalt er natuurlijk niet om dat er een nieuwsgierige nerd naar em zit te koekeloeren vanuit verschillende hoeken. Dat is het kernidee achter een tensor: een tensor is een meetkundig voorwerp dat je vanuit verschillende invalshoeken kunt bekijken. Bij elke invalshoek LIJKT de tensor anders te zijn, maar als meetkundig voorwerp verandert het niet.
Wat anders LIJKT zijn de zogenaamde componenten van de tensor. En de invalshoek is wat wiskundigen een “coördinatenstelsel” noemen. Dat idee gaan we nu wiskundig bekijken aan de hand van de meest bekende tensor in tensorland: de vector in het platte vlak.
Zo plat als een dubbeltje
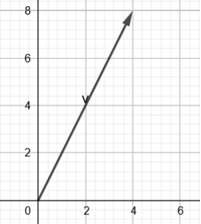
Je ziet in de afbeelding links een vector in het vlak getekend: een ding met een richting en een grootte. Natuurkundig kan deze vector van alles voorstellen: een kracht, een verplaatsing, een snelheid…noem maar op.
Maar als je er aan wilt rekenen, dan moet je een coördinatenstelsel aanleggen. Als jij bijvoorbeeld wilt beschrijven met wat voor snelheid een kanonskogel wordt weggeschoten, dan kun je als coördinatenstelsel een rechthoekig stelsel nemen met het kanon in de oorsprong. Je mag ook jezelf als oorsprong nemen als je dat gemakkelijker vindt of een groot ego hebt. Dit coördinatenstelsel definieert de componenten van de vector. Vaak kiezen we de assen van het coördinatenstelsel loodrecht op elkaar, omdat we dan de stelling van Pythagoras kunnen toepassen als we de lengte van de vector willen uitrekenen. Maar nogmaals: de vector maalt niet om onze zucht naar rekengemak; de assen hoeven dus zeker niet loodrecht op elkaar te staan.
Coördinaten en basisvectoren
Het coördinatenstelsel definieert twee zogenaamde basisvectoren. Elke vector in het vlak kan als een combinatie van deze twee basisvectoren worden geschreven. Het feit dat we daarvoor twee basisvectoren nodig hebben laat ons zeggen dat het vlak tweedimensionaal is. Laten we voor het gemak de basisvectoren kiezen als e1 = (2,0) en e2 = (0,2). Vervolgens kunnen we de componenten van de vector bepalen in dit stelsel. Je ziet in dit plaatje dat de vectortop (x,y) coördinaten gelijk aan (4,8) heeft, zodat V = 2e1 + 4e2. We zeggen dat de componenten van de vector in dit coördinatenstelsel gelijk zijn aan (2,4): 2 stapjes in de e1 richting en 4 stapjes in de e2 richting.
Maar nu kijkt er iemand over je schouder mee, en die persoon wil liever dat jij als basisvectoren (1,0) en (0,1) kiest. Oftewel: hij wil de lengte van beide basisvectoren halveren. Dat is prima, maar dan moeten de componenten van de vector worden verdubbeld van (2,4) naar (4,8): vier stapjes in de nieuwe e1-richting en acht stapjes in de nieuwe e2-richting. Anders zou de vector als geheel immers veranderen, terwijl we eerder zeiden dat de vector niet maalt om onze coördinatenkeuze! Je ziet dus het volgende: als je je coördinatenstelsel oftewel basisvectoren verandert, dan veranderen de componenten van je vector in tegengestelde richting! Dit blijkt heel algemeen te zijn. We kunnen dit wat concreter maken door de vector te ‘ontbinden’ in de basisvectoren:
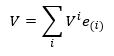
waarbij de haakjes in de basisvector e(i) aangeven dat de i-index hier een hele vector labelt, en niet slechts een component ervan. Omdat de vector V niet maalt om onze coördinatenkeuze, moet na een transformatie gelden dat

Een check voor ons getallenvoorbeeld waarbij we beide basisvectoren in lengte halveerden: er moet dan blijkbaar gelden dat

En dat klopt:
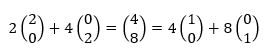
We kunnen ons coördinatenstelsel echter ook draaien over een hoek van, zeg, 45 graden. Daardoor veranderen de basisvectoren, waarvoor je de wiskundige uitdrukking weer kunt opschrijven. De componenten van de vector veranderen dan weer tegengesteld aan deze draai. Of we kunnen de oorsprong van ons stelsel opschuiven. We kunnen zelfs overgaan op zogenaamde poolcoördinaten. Ook dan veranderen de componenten van de vector. Maar altijd weer tegengesteld aan de verandering van de basisvectoren, zodat de vector als geheel hetzelfde blijft. Je ziet dat het bij tensoren dus erg belangrijk is om te kijken hoe de componenten en basisvectoren transformeren onder een verandering van coördinaten.
Combineren kun je leren
Een erg belangrijke eigenschap van een vector is dat de nieuwe componenten combinaties zijn van de oude componenten. En niet zomaar combinaties, maar lineaire combinaties. Als je de nieuwe componenten uitdrukt in de oude componenten, dan zul je dus de oude componenten niet gekwadrateerd of met worteltekens zien. In formulevorm zien de nieuwe componenten er zo uit:
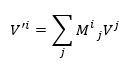
De komma stelt het nieuwe coördinatenstelsel voor. De matrix M beschrijft de transformatie en wordt bepaald door hoe je de basisvectoren precies verandert. De componenten van de vector zullen dan tegengesteld veranderen. Dat volgt uit onze eis dat de vector V zelf ongemoeid blijft na de transformatie. Bij de transformatie heffen de verandering van de vectorcomponenten en de verandering van de basisvectoren elkaar op zodat de vector hetzelfde blijft. Wiskundig: de basisvectoren transformeren met de inverse van M en de vectorcomponenten met M zelf, zodat de vector V als geheel invariant blijft.
Als je onwennig bent met matrices en sommatietekens, dan kunnen we de transformatieformule ook uitschrijven per component:
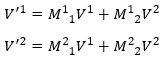
Je ziet: de nieuwe componenten V‘i zijn lineaire combinaties van de oude componenten Vi. In het bijzonder zie je dat als je de nulvector neemt (de vector waarbij elke component nul is) en deze vervolgens in het nieuwe stelsel bekijkt, de nieuwe componenten ook nul zijn:
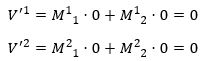
Lineaire combinaties van nullen leveren immers gewoon weer nul op. Oftewel: de nulvector blijft hetzelfde na een transformatie.
Wie niet snel is moet traag zijn
Bij zoveel termen helpt een concreet voorbeeld. In ons eerdere voorbeeld waarbij we de basisvectoren halveerden moesten we allebei de componenten juist verdubbelen. Dat ziet er voor de vectorcomponenten zo uit:
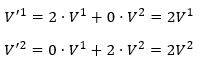
De matrix M is dus een matrix met 2’en op de diagonaal. Maar je ziet dat we veel algemenere transformaties kunnen bekijken. Ik heb de vector de letter V meegegeven, en dit kan van alles zijn: een kracht, een snelheid, noem maar op. Als we in drie richtingen kijken, dan hebben deze vectoren drie componenten in plaats van twee. Dat is gewoon een kwestie van wat meer ruimte reserveren voor de vector. Maar er zijn ook grootheden waarbij een vector onnodig is. Een simpel voorbeeld: de temperatuur. De temperatuur in een kamer heeft geen richting, alleen een grootte. De temperatuur kan natuurlijk wel van plek tot plek veranderen. Maar wiskundig zouden we de temperatuur dus beschrijven als een functie T(x,y,z) van de plaatscoördinaten {x,y,z}. We noemen dit type tensor een scalair. Een nog simpeler voorbeeld van een scalair is de massa van een voorwerp. Die is zelfs constant (als het voorwerp natuurlijk geen massa verliest)! Als we verschillende coördinatenstelsels gebruiken, oftewel verschillende waarnemers die naar hetzelfde voorwerp kijken, dan blijft de massa van het voorwerp hetzelfde. Logisch ook, want de hoeveelheid atomen waaruit het voorwerp bestaat verandert niet per waarnemer.
Er zijn daarentegen ook grootheden waarbij we juist meer componenten nodig hebben. Eén zo’n grootheid is de zogenaamde traagheidstensor. Net zoals een kracht voor een versnelling zorgt, zal een krachtmoment voor een draaiversnelling zorgen. Een krachtmoment is een kracht die je op een voorwerp uitoefent dat kan draaien. Denk bijvoorbeeld aan het openen van een deur. Het krachtmoment is dan ruwweg de kracht die je uitoefent maal de afstand van je hand tot de scharnier. Daardoor zal de deur gaan draaien.
Om de draaiversnelling uit te rekenen gebruik je de traagheidstensor van in dit geval de deur. Als het voorwerp niet symmetrisch is, of je draait het voorwerp niet rond een symmetrie-as zoals bij onze deur, dan blijkt de traagheidstensor 9 componenten te hebben. Eigenlijk zijn hiervan maar zes onafhankelijk van elkaar, maar dat is voor ons niet zo belangrijk. We hebben dus een soort uitbreiding nodig van een vector, een tensor met twee indices in plaats van één. Laten we deze tensor domweg T noemen. De componenten zijn dan Tij . Elke letter i of j kan drie waarden aannemen als we in drie dimensies werken, dus er zijn inderdaad 3×3=9 componenten.
Trage transformaties
Nu de hamvraag: hoe transformeren deze componenten als we naar een nieuw coördinatenstelsel gaan? Hoe ziet de traagheidstensor er bijvoorbeeld uit voor een waarnemer die rond de deur gedraaid is? Het antwoord: de tensor transformeert alsof het een product is van twee vectoren! Let op: alsof! De tensor zelf hoeft dus niet zo’n product te zijn; we kunnen er alleen de transformatie eigenschappen uit herleiden. Hoe ziet dat eruit? Wel, we weten ondertussen dat de componenten van een vector V transformeren als
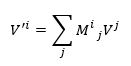
Dus als we daar nog een vector W tegen aan knallen, dan transformeert het product van beide vectoren als
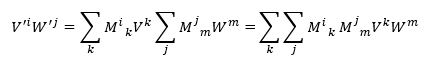
Per definitie transformeert een tensor met twee indices ook zo:
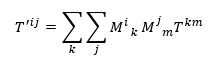
Als je dit uitschrijft, dan zie je dat elke nieuwe component weer een lineaire combinatie van de oude componenten is. De nieuwe 11-component van de tensor wordt bijvoorbeeld
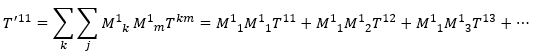
waarbij we negen termen in totaal krijgen voor elke nieuwe component: elke nieuwe component is dus een lineaire combinatie van alle negen oude componenten. De componenten van de matrix M kun je opnieuw uitrekenen als je de precieze transformatie tussen de oude en nieuwe basisvectoren weet: de componenten van de vector zullen dan wederom tegengesteld veranderen. En ook hier geldt weer: als alle componenten van de tensor nul zijn in één coördinatenstelsel, dan zullen ze dat ook allemaal in het nieuwe coördinatenstelsel zijn. Een lineaire combinatie van nullen levert immers gewoon weer nul op.
Je kunt je onze tensor voorstellen als een matrix van getallen, maar pas op: de matrix stelt de componenten Tij voor in een bepaalde basis. We weten ondertussen dat een tensor een object is dat niet maalt om onze coördinaatkeuze. Dus een tensor als slechts een matrix bestempelen zou de tensor geen recht doen. Tensoren hebben veel meer structuur! Je zou je ook nog kunnen afvragen wat de precieze basis is waarin we onze tensor opschrijven. Dat blijkt het product te zijn van twee basisvectoren, wat ook weer een matrix oplevert. De “basistensoren” voor onze tensor T kunnen we dus ook opschrijven als matrices.
We kunnen dit idee ook nog uitbreiden naar meer indices. En er blijken bovendien tensoren te zijn met indices beneden. Om de oorsprong daarvan te begrijpen moeten we tensoren als multilineaire afbeeldingen bekijken die inwerken op vectoren en zogenaamde ‘duale vectoren’. Daaruit volgen alle transformatie-eigenschappen, en deze objecten hebben ook weer allerlei toepassingen. In het bijzonder komt hier het zogenaamde ‘inproduct’ tussen vectoren vandaan. De details hiervan laat ik achterwege.
Newton
Tot slot een belangrijke toepassing: de tweede wet van Newton. Deze wet zegt dat de resulterende kracht op een voorwerp gelijk is aan de massa maal de versnelling van het voorwerp. In vectorvorm wordt dat
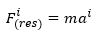
Stel dat er volgens jou geen resulterende kracht op het voorwerp werkt, zoals een koffiemok die op tafel staat. De snelheid van de mok is dan constant (namelijk: 0 m/s) en dan geldt dus dat Fres =0. Er is een krachtenevenwicht omdat de zwaartekracht van de aarde op de mok de normaalkracht van de tafel op de mok opheft. Maar stel nu dat je vervolgens de mok vanuit een andere hoek bekijkt door bijvoorbeeld een kwartslag om de mok te draaien. Dan geldt in het nieuwe (met komma aangegeven) coördinatenstelsel
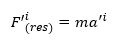
wat je kunt aantonen door de tweede wet van Newton met een rotatie(matrix) te draaien. We hebben geen komma bij de massa gezet, omdat we zagen dat de massa voor elke waarnemer hetzelfde is: m’=m. Maar we zagen ook dat de nulvector transformeren opnieuw de nulvector oplevert. We mogen dus concluderen dat ook in het gedraaide stelsel de resulterende kracht nul zal zijn, en dus ook de versnelling van de mok. Dat zal hopelijk geen grote verrassing voor je zijn: door te draaien hef je het evenwicht tussen zwaartekracht en normaalkracht immers niet op. We noemen de tweede wet van Newton daarom een tensorvergelijking.
Tot nu toe zagen we eenmalige transformaties in de ruimte. We kunnen echter ook een transformatie uitvoeren naar een waarnemer die een constante snelheid heeft ten opzichte van jou in, zeg, de x-richting. De waarnemer beweegt dan in de ruimte. Dat is een tijdsafhankelijke transformatie, want als ik de mok een coördinaat x meegeef, dan zal de reizende waarnemer een coördinaat
x’ = x + vt aan de mok meegeven. Ook daarvan kun je de bijbehorende transformatie van de vectorcomponenten opschrijven, en dan blijkt opnieuw dat jouw nulvector getransformeerd wordt naar een nieuwe nulvector. Wiskundig komt dit omdat de versnelling de tweede tijdsafgeleide van de plaats (hier: x) is, en als de tweede tijdsafgeleide van x verdwijnt, dan verdwijnt de tweede tijdsafgeleide van x’ = x + vt (de plaatscoördinaat die de reizende waarnemer voor de mok gebruikt) ook. Natuurkundig kun je dit begrijpen omdat de reizende waarnemer zal zien dat de mok met een constante (!) snelheid v van hem afreist, waardoor de versnelling nog steeds nul zal zijn en de resulterende kracht dus ook.
Maar pas op: dit verandert als we de reizende waarnemer laten versnellen! De versnelde waarnemer zal dan vanuit zijn stelsel concluderen dat de mok versnelt, en dat er dus een kracht op het voorwerp moet werken. De tweede wet van Newton is dan geen tensorvergelijking meer: waar de stilstaande waarnemer concludeerde dat Fres = 0 zal de versnelde waarnemer concluderen dat dit niet meer zo is. Natuurkundig komt dat omdat de versnelde waarnemer stilstaat in zijn eigen stelsel (duh…) en zijn versnelling en daarmee de resulterende kracht op hem dus toedicht aan de koffiemok!
We kunnen dus concluderen dat we bij een tensorvergelijking altijd de desbetreffende transformaties moeten benoemen. De transformaties waarbij de tweede wet van Newton als een tensor transformeert zijn opschuivingen in de ruimte en tijd, constante draaien in de ruimte, en de transformatie naar een stelsel dat met een constante snelheid t.o.v. jou bewegen. Wiskundigen noemen deze groep van transformaties de Galilei-groep. Elke transformatie kunnen we associeren met een waarnemer. Als één zo’n waarnemer concludeert dat de resulterende kracht op een voorwerp nul is, dan zullen alle andere waarnemers dat ook doen. Voorbeelden waarbij dat niet zo is zijn de eerdergenoemde versnelling of wanneer we een waarnemer met een constante hoeksnelheid laten ronddraaien.
Komt tijd, komt relativiteit
Je ziet dat we dus domweg relativiteit beschrijven: hoe kijken verschillende waarnemers naar dezelfde gebeurtenissen, wat verandert hierbij en wat blijft hetzelfde? Tensoren zijn daarvoor dus uitermate geschikt. In Einsteins algemene relativiteit worden de vergelijkingen voor het zwaartekrachtsveld bijvoorbeeld als een vier bij vier tensor geformuleerd, en is dit een tensorvergelijking voor elke waarnemer! Uiteindelijk zijn, net als bij de traagheidstensor, niet alle vergelijkingen onafhankelijk en blijven er tien over. Die overigens nog steeds waanzinnig ingewikkeld zijn.
Dat zegt ons meteen waarom tensoren zo belangrijk zijn in de natuurkunde. Want heel vaak hebben we te maken met verschillende gezichtspunten, en dan moeten we weten hoe we deze gezichtspunten in elkaar vertalen. Een eenvoudig voorbeeld is het weer: we moeten begrijpen hoe wij als ronddraaiende waarnemers op het aardoppervlak bewegende luchtstromen beschrijven. Dezelfde soort berekeningen als hierboven geven dan bijvoorbeeld dat deze luchtstromen ten opzichte van ons afbuigen, wat we verklaren met de zogenaamde Coriolis- en centrifugaalkracht. Of denk aan een vrije val: als jij meevalt met een voorwerp in een vacuüm, dan staat het voorwerp stil ten opzichte van jou en is de zwaartekracht op het voorwerp volgens jou dus plots opgeheven! Dit inzicht leidde Einstein naar het zogenaamde “equivalentieprincipe” dat het hart vormt van zijn algemene relativiteitstheorie. Of, zoals hij het zelf noemde: zijn “meest gelukkige gedachte”.
Je ziet: het kan lonen om eens van gezichtspunt te veranderen.
Geef een reactie